Accurate and cost-effective cavity-modified quantum dynamics from classical-like trajectories

Maximilian Saller, Yifan Lai, Eitan Geva

Department of Chemistry, University of Michigan, Ann Arbor

Cavity

Ebbesen et al., Angw. Chem., 51, 1592-1596 (2012)

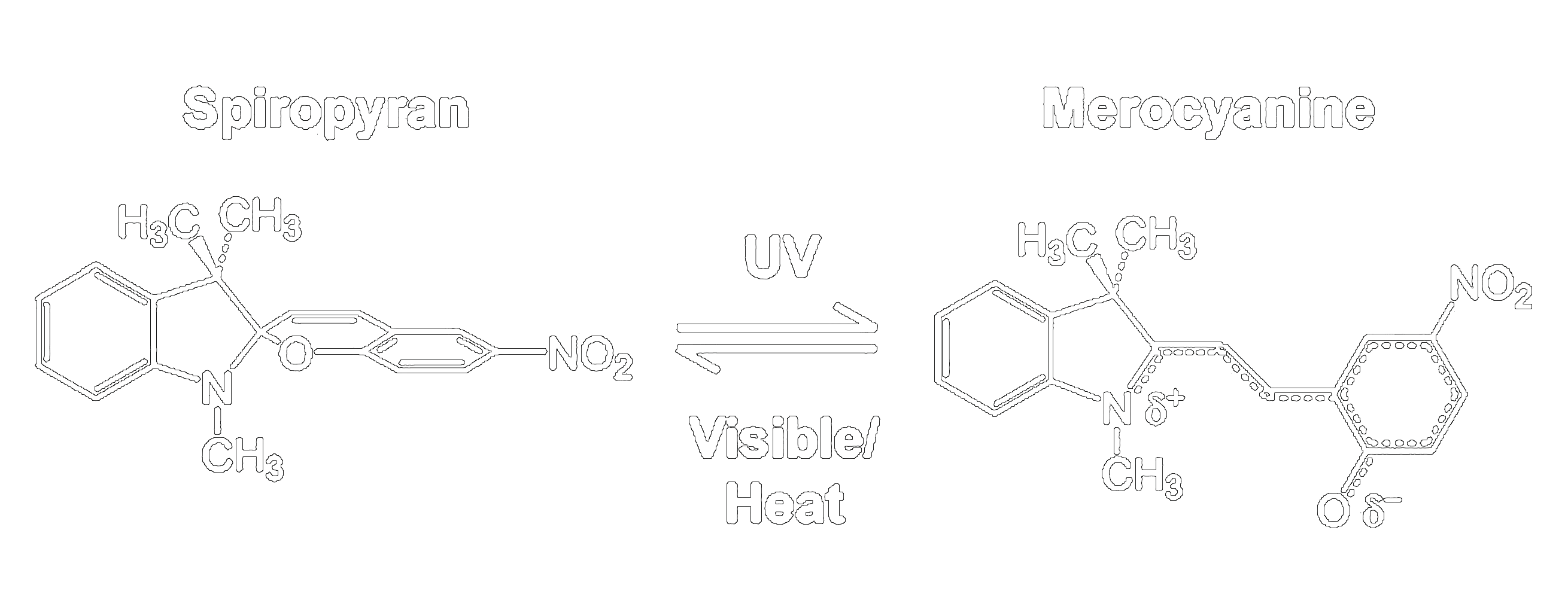
Ebbesen et al., Phys. Rev. Lett., 106, 196405 (2011)

Ebbesen et al., Angw. Chem., 51, 1592-1596 (2012)

Ebbesen et al., Phys. Rev. Lett., 106, 196405 (2011)

Ebbesen et al., Angw. Chem., 51, 1592-1596 (2012)

Ebbesen et al., Chem. Phys. Chem., 14, 125-131 (2013)

Ebbesen et al., Phys. Rev. Lett., 106, 196405 (2011)

Ebbesen et al., Angw. Chem., 51, 1592-1596 (2012)

Ebbesen et al., Chem. Phys. Chem., 14, 125-131 (2013)

Ebbesen et al., Acc. Chem. Res., 49, 2403-2412 (2016)

Ebbesen et al., Phys. Rev. Lett., 106, 196405 (2011)

Ebbesen et al., Angw. Chem., 51, 1592-1596 (2012)

Ebbesen et al., Chem. Phys. Chem., 14, 125-131 (2013)

Ebbesen et al., Acc. Chem. Res., 49, 2403-2412 (2016)

Ebbesen et al., Science, 363, 615-619 (2019)

Trajectories

\[ P_{\ket{\alpha}\!\bra{\alpha}\rightarrow\ket{\beta}\!\bra{\beta}} (t) = C_{\alpha\beta}(t) = \mathrm{Tr}\Big[ \hat{\rho}_{\mathrm{nuc}}\ket{\alpha}\!\bra{\alpha} \mathrm{e}^{\mathrm{i}\hat{H}t}\ket{\beta}\!\bra{\beta} \mathrm{e}^{-\mathrm{i}\hat{H}t} \Big] \]

\[ C_{\alpha\beta}(t) \approx \frac{1}{(2\pi)^{F+S}} \iint\iint \rho^W_\mathrm{nuc}(x, p) P_\alpha^W(X,P) P_\beta^W(X(t), P(t))~ \mathrm{d}x\,\mathrm{d}p\,\mathrm{d}X\,\mathrm{d}P \]

Some Mapping methods you may have heard of

Mean Field (Ehrenfest)

PBME (LSC I) LSC-IVR (LSC II)

mLSC Windowing (SQC)

Spin Mapping

FBTS PLDM

MACS, A. Kelly and J. Richardson, J. Chem. Phys., 150, 071101 (2019)

MACS, A. Kelly and J. Richardson, Farad. Discus., 221, 150-167 (2020)

Quantum Dynamics

Simple Matter - Hard Cavity

\[ \hat{H} = \left( \begin{array}{cc} \varepsilon_1 & 0 \\ 0 & \varepsilon_2 \\ \end{array}\right) + \sum\limits_{j=1}^{\textcolor{red}{200}} \mu \omega_j \lambda_j \textcolor{red}{R_j} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array}\right) + \sum\limits_{j=1}^{\textcolor{red}{200}} \hbar \omega_j a^{\dagger}_j a_j \]

a 3-level version

Simple Matter - Hard Cavity

2-level system

MACS, A. Kelly and E. Geva, J. Chem. Phys. Lett., 12, 3163-3170 (2021)

Simple Matter - Hard Cavity

3-level system

MACS, A. Kelly and E. Geva, J. Chem. Phys. Lett., 12, 3163-3170 (2021)

Hard Matter - Simple Cavity

\[\begin{align*} \hat{H} = &\left( \begin{array}{cc} 0 & \Delta \\ \Delta & -\varepsilon \\ \end{array}\right) + \frac{1}{2} \left[ \frac{P_s^2}{M_s} + M_s \omega_s^2\left( \begin{array}{cc} R_s^2 & 0 \\ 0 & (R_s - R_\mathrm{A}^0)^2 \end{array}\right) \right]\\ &+ \frac{1}{2} \sum\limits_{j=1}^{\textcolor{red}{100}} \frac{P_j^2}{M_j} + m_j \omega_j^2 \Big(R_j - \frac{c_j}{M_j \omega_j^2}R_s \Big)^2\\ &+ \hbar g_c (a^{\dagger}_c + a_c) \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array}\right) + \hbar \omega_c a^{\dagger}_c a_c \end{align*}\]

Hard Matter - Simple Cavity

\[k_{\mathrm{D}\to\mathrm{A}} = \int \mathrm{e}^{\mathrm{i}\varepsilon t} C_{FGR} (t) ~\mathrm{d}t\]

\[C_{FGR} (t) = \mathrm{Tr}\Big[\hat{\rho}^{eq} \mathrm{e}^{\mathrm{i}\hat{H}_{\mathrm{D}}t} \hat{\Gamma}_{\mathrm{DA}}\mathrm{e}^{-\mathrm{i}\hat{H}_{\mathrm{A}}t} \hat{\Gamma}_{\mathrm{DA}}\Big]\]

Hard Matter - Simple Cavity

LSC + FGR can give exact results

MACS, Y. Lai and E. Geva, J. Chem. Phys. Lett., 13, 2330-2337 (2022)

Take home message

Classical-like trajectories can yield accurate results for cavity-modified quantum dynamics.

Since they scale linearly with system size they can access large, complex and multiple molecules and multiple cavity modes.

"Accurate and cost-effective cavity-modified quantum dynamics from classical-like trajectories"

Thanks

Prof. Eitan Geva

[Dr] Yifan Lai

Prof. Jeremy Richardson (ETH Zurich)

Dr Aaron Kelly
(MPI Hamburg)